Вариант № OLYMP_2901
Добавлен 28 октября 2018 г. в 0:00. Изменён 28 октября 2018 г. в 0:00. Скачать PDF
Скачать PDF1 2 3 4 5
Задача 1. Улица
Задание
По одну сторону улицы находятся дома с нечётными номерами (1, 3, 5, …), по другую сторону – с чётными (2, 4, 6, ...). Дом №1 находится напротив дома №2, дом №3 – напротив дома № 4 и т. д. До соседнего дома нужно идти вдоль по улице одну минуту, неважно, с какой стороны улицы он находится (то есть от дома №1 нужно идти одну минуту как до дома №3, так и до дома №4). До дома, стоящего напротив, идти не нужно.
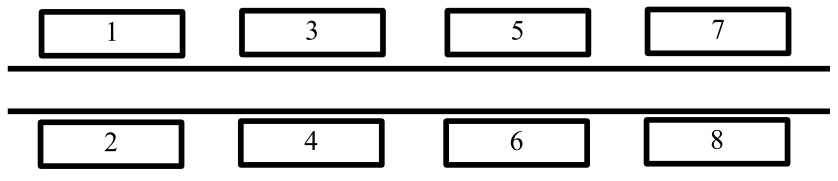
Человек вышел на улицу из дома номер A и должен дойти до дома номер B.
Определите, сколько минут ему нужно идти вдоль по улице.
Программа получает на вход два различных целых положительных числа A и B, не превосходящие 2×109, – номера домов.
Программа должна вывести одно число – искомое количество минут.
Решение
Рассмотрим все 4 возможных случая:
- начальный дом с чётным номером, конечный дом с чётным номером;
- начальный дом с нечётным номером, конечный дом с нечётным номером;
- начальный дом с чётным номером, конечный дом с нечётным номером;
- начальный дом с нечётным номером, конечный дом с чётным номером.
Если дома имеют одинаковую чётность (случаи 1 и 2), расстояние между домами с номерами a и b (заметим, что необязательно a < b!) можно определить как
dist := abs(b — a) div 2,
где abs обозначает операцию взятия модуля числа, а div обозначает операцию целочисленного деления.
Например, расстояние между домами с номерами 3 и 7 будет равно (7 — 3) div 2 = 2.
Если дома имеют разную чётность (случаи 3 и 4), рассмотренная выше формула будет работать не всегда корректно.
Например, расстояние между домами с номерами 3 и 4 (или 4 и 3) будет равно (4 — 3) div 2 = 0, что не правильно.
Первый способ решения предполагает отдельное рассмотрение случаев 1, 2 и 3, 4 соответственно. В качестве упражнения проделайте это самостоятельно, используя условный оператор.
Второй способ решения предполагает сведение случаев 2, 3 и 4 к случаю 1 (номера обоих домов – чётные). Действительно, расстояние между домами 3 и 5; 4 и 5; 3 и 6 такое же, как между домами с номерами 4 и 6. Легко заметить, что каждое нечётное число заменилось следующим за ним чётным.
Как подобный приём лучше реализовать в программе? Можно предложить разные способы (например, вещественное деление на 2, округление вверх и умножение результата на 2), но мы рассмотрим следующий.
Пусть имеется натуральное число n и, если оно нечётное, необходимо сделать его чётным (то есть получить n + 1).
Прибавим к исходному числу n единицу и нацело поделим полученную сумму на 2.
Полученный результат будет одинаков как для нечётного, так и для чётного n.
Например, при n = 7 и n = 8 получим:
(7 + 1) div 2 = (8 + 1) div 2 = 4.
Умножая результат целочисленного деления на 2, получим искомое чётное число.
В примере выше 4 * 2 = 8.
Программная реализация на Python3 при рассмотренном способе решения занимает ровно одну строку:
print(abs((int(input()) + 1) // 2 * 2 - (int(input()) + 1) // 2 * 2) // 2)
При использовании тернарного оператора ?: достаточно оригинальной является реализация программы на языке С++:
#include <iostream>
using namespace std;
int main() {
int a, b;
cin >> a >> b;
cout << abs((a % 2 ? a + 1 : a) - (b % 2 ? b + 1 : b)) / 2;
return 0;
}
 Олимпиады
Олимпиады